pKa
Chapter 2 provides an overview of the underlying theory surrounding pKa. Briefly, the acidity of organic compounds is widely recognised as an important property, particularly with respect to pharmaceuticals (Liao and Nicklaus, 2009; Lee and Crippen, 2009). Liao and Nicklaus (2009), suggest that along with the partition coefficient, solubility, and reaction rate, pKa is a critical parameter used in drug formulation, since the degree of ionisation influences the solubility, dissolution rate, and gastrointestinal uptake into the bloodstream of an API. Consequently, large datasets of measured pKa values for organic acids are available (for instance, Kortüm et al, 1960; Perrin, 1965; Serjeant and Dempsey, 1979; Dean, 1999; Lide, 1995). The majority of pKa values are reported at 20 or 25°C, and at a given ionic strength, consequently, reported pKa values may vary by about 0.3 pKa units.
Estimation methods for pKa have a relatively long history, with early approaches utilising empirical methods. For instance, Hammett (1940) introduced the use of a constant, which would account for the effect of substituents in either the meta- or para- position on the standard free energy change of dissociation of the carboxyl group. Consequently, linear free energy relationships (LFERs) that utilise Hammett Constants represent an important group of pKa estimation methods (Lee and Crippen, 2009). QSARs represent another group of estimation methods, whereby structural descriptors are defined as a tool for estimating pKa, as are read-across methods that attempt to predict the pKa of an unknown based on similarity in structure to a compound with a measured pKa value (Lee and Crippen, 2009). More recently, quantum chemical methods have been developed, which attempt to predict pKa from first principles (Liao and Nicklaus, 2009; Yu et al, 2011). The methods reviewed in this report each utilise an empirical approach.
ACD/pKa DB
The ACD/pKa DB uses a fragment-based approach for estimating pKa values. The commercially available software consists of chemical structure fragments, and uses a proprietary algorithm to calculate predicted values for whole molecules based on its constituent fragments. pKa values are derived using Hammett-type equations for more than 650 ionising centres (Manchester et al, 2010). The method is also extensively parameterised with more than 3,000 substituent constants and incorporates methods for estimating substituent effects for species outside the training set (Manchester et al, 2010). For instance, the commercial software has an option for adding proprietary experimental data, which can help improve the prediction accuracy for chemicals not adequately captured within the library. Additionally, an algorithm is implemented for estimating apparent pKa values for multiprotic compounds, which can cause discrepancies between the predicted and measured values when the pKa values of different ionising groups on the compound are within 1 to 2 log units (Manchester et al. 2010). More information regarding the ACD/pKa DB can be found at www.acdlabs.com/physchem/.
Liao and Nicklaus (2009), Meloun and Bordovská (2007), and Manchester et al (2010) all observed that estimates of pKa using the ACD/pKa DB perform relatively well, especially when compared to other fragment-based approaches.
SPARC
As described above, the fundamental approach used by SPARC is based on a blending of linear free energy relationships (LFERs), structure activity relationships, and perturbed molecular orbitals (PMO) to describe a variety of physical and reactivity parameters (Hilal et al, 2004). As with the estimation of other properties, the molecular structure of a chemical input to SPARC, is classified into functional units defined as either a reaction centre or perturber (Hilal et al, 1996). The reaction centre (C) is the smallest subunit that has the potential to ionise and lose a proton to the solvent. The perturber (P) is the molecular structure appended to C. The perturber structure is assumed to be unchanged in the reaction. The pKa value of an ionisable organic is expressed in terms of the contributions of both P and C:
Where (pKa)C describes the ionisation behaviour of the reaction centre, and äP(pKa)C is the change in ionisation behaviour brought about by the perturber structure. SPARC computes reactivity perturbations that are then used to correct the ionisation behaviour of C in terms of potential mechanisms for interaction of P and C as:
More information about SPARC for estimating pKa and its use in estimating pKa values for relatively large numbers of chemicals is given in Hilal et al (1994; 1995) and more recently by Meloun and Bordovská (2007).
Pipeline PilotTM
A topological method is utilised in the Accelrys Pipeline PilotTM software package, in which ionising centres are captured using what is referred to as ‘path fingerprints' (Manchester et al, 2010). The Pipeline PilotTM program consists of six models, trained on about 12000 chemicals, which are used to classify aliphatic and aromatic acids and bases, phenols, and heterocyclic amines. If a test compound cannot be classified into one of the six groups, then a generic model based on either all acids or all bases is used. The models correlate the presence of specific paths of up to six atoms from an ionising centre with the difference in pKa of that centre relative to the mean for its respective category (Manchester et al, 2010). More information about Pipeline PilotTM can be found at http://accelrys.com/products/pipeline-pilot/.
Comparison of pKa estimation methods
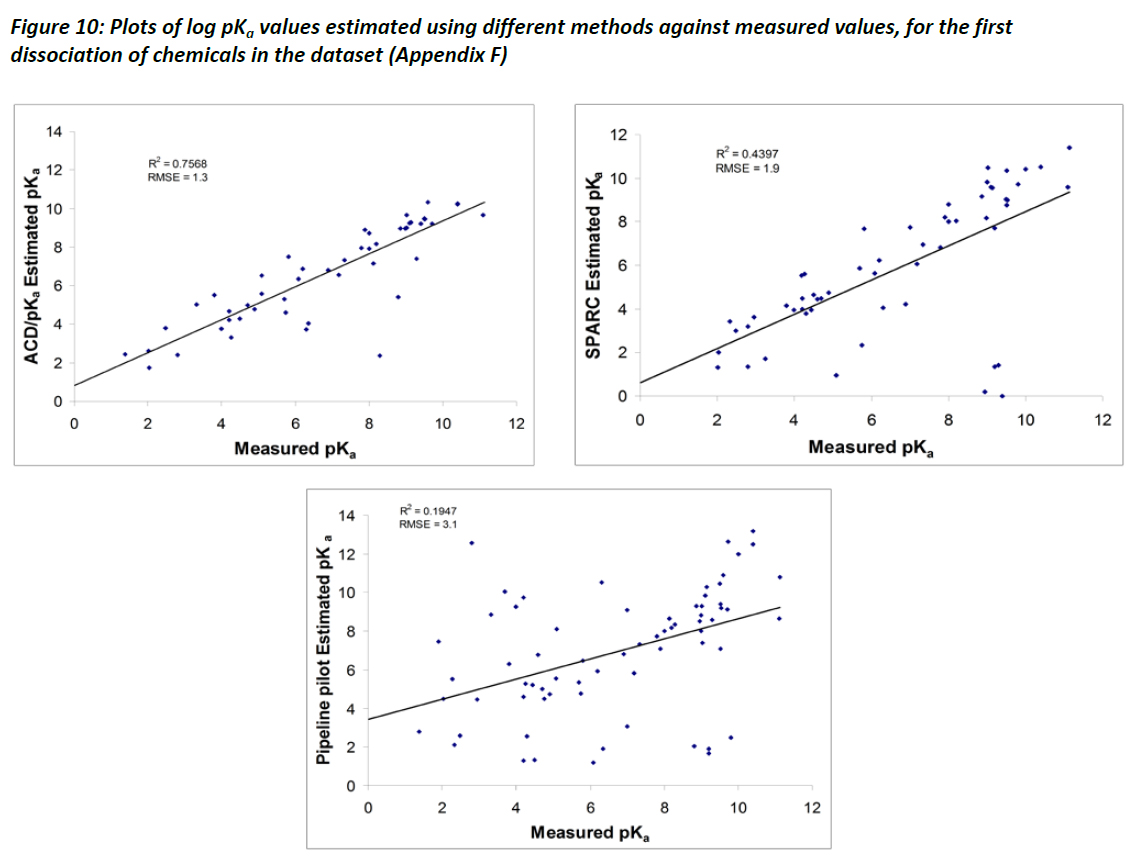
Figure 10 summarises the comparison of methods against measured values for data listed in Appendix F. Generally, the ACD/pKa method performed relatively better than both SPARC and Pipeline Pilot, which is consistent with observations by Liao and Nicklaus (2009). The relationships shown in Figure 10, however, tend to be poorer than those reported by Liao and Nicklaus (2009). Two possible reasons are suggested for why the observed discrepancy may exist. First, the current comparison between measured data and estimation methods is not as thorough as that by Liao and Nicklaus (2009), in that no attempt was made to identify the individual protonation sites for each of the molecules included in the dataset. Rather, a simple comparison was made of the first dissociation constants between the measured data and the estimation programs. Closer examination of the data suggests that in some instances the measured data may not be as robust as the estimation method in defining the first dissociation constant, and it may be that the data are limited to reporting pKa data within a physiologically relevant pH range (typically at pH of 7.4). Thus, there are some concerns regarding the accuracy of the measured data. Second, Liao and Nicklaus (2009) as well as Balogh et al (2009) observed that several of the estimation methods for pKa performed significantly poorer when estimating pKa values for chemicals with protonation sites in the pKa range of 5.4 to 9.4, including ACD/pKa, Pipeline Pilot, and SPARC. Nevertheless, Liao and Nicklaus ,(2009) observed that most of the estimation methods they assessed performed generally very well, and suggest that they are useful tools in drug development.
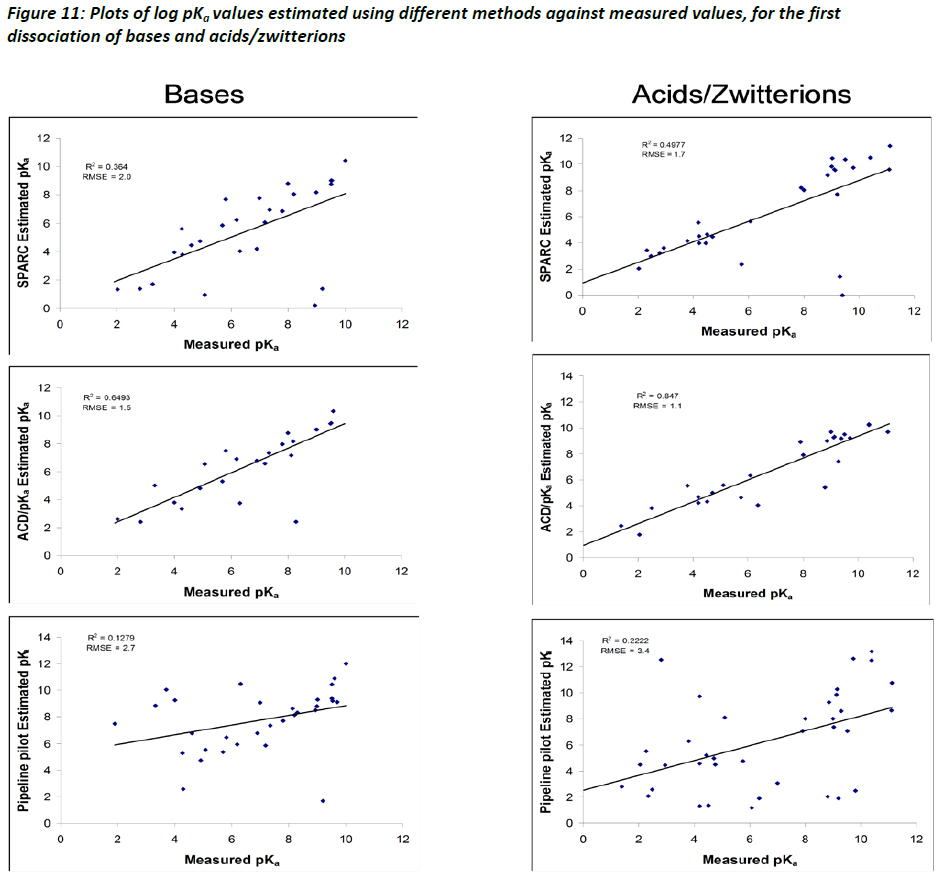
When comparing the performance of the different methods for bases as opposed to acids and zwitterions, it is interesting to see that most methods tend to show poorer performance when predicting pKa values of bases, but do relatively well when just predicting pKa of acids and zwitterions. Figure 11 illustrates these different relationships. It is unclear what might be driving this observation, but even with the relatively small dataset, it is of interest to note that the observation is consistent with results reported by Yu et al (2011). It is further demonstrated that both ACD and SPARC are prone to error when encountering ortho- substitution of aromatics and intramolecular H-bonding accompanying ortho- substitution (Yu et al, 2011).
A number of recent studies, in addition to that of Liao and Nicklaus (2009), have provided additional assessments between various estimation methods (see for instance Meloun and Bordovská (2007); Balogh et al (2009); Manchester et al (2010); Yu et al (2011)). The ACD/pKa method consistently performs better than the three other estimation methods. Thus, the predictions based on ACD/pKa are likely to be more accurate than other methods, which is an important factor when utilising pKa data in the estimation of log DOW. As a way to increase the level of confidence, the TF also supports the recommendation of Yu et al (2011) who suggest a consensus modelling approach, which would combine output from ACD and SPARC, whereby similar predictions between the two methods would provide a lower level of uncertainty.